Abstract
Fractals are geometric shapes with detail at any scale. Many fractals are self-similar. What this means is that it is possible to zoom into any part of it, and it will look like the whole object. A classic example of a fractal is the Mandelbrot Set. My summer project involved constructing families of fractals through “Schottky groups”, by nesting various circles inside circles, an infinite number of times. Fractals are visually beautiful, and it also provides insight to why many people love and study mathematics.
Creating beautiful, intricate patterns with mathematics
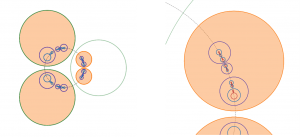
Fractals are geometric shapes with detail at any scale. Many fractals are self-similar. What this means is that it is possible to zoom into any part of it, and it will look like the whole object. A classic example of a fractal is the Mandelbrot Set. Some objects in real life such as leaves and coastlines are approximately fractals, having detail up to relatively small scales. My project involved constructing fractals through the so-called Schottky groups.
Fix an even number of circles in the (complex) plane. Schottky groups define certain transformations on this plane. Mainly, it allows circles to be mapped into other circles, creating a nesting of circles. By applying multiple of these transformations, this creates multiple nestings of circles inside each other. Doing this an infinite number of times creates an infinite nesting of circles, and taking all of the smallest circles (which have shrunk to become points) creates a fractal. My summer project involved looking at a family of Schottky groups, and investigating properties of the different fractals.
Many people find mathematics difficult to understand, especially after high school level, which is where most people stop doing mathematics completely. Advanced mathematics becomes very abstract, and Greek letters start appearing more than numbers. But what is the purpose of studying maths?
Mathematics itself is a broad field. There is pure, applied, and statistical maths. Statistical maths uses mathematical techniques to study data and draw conclusions. Applied maths applies maths to other fields, such as physics, engineering, medicine. Pure maths studies theoretical ideas inside maths, without necessarily having applications in real life. I study pure maths, and this project is a pure maths project. What is the purpose of studying pure maths?
Although pure maths is studied with no intention for applications, history has shown that in fact many applications have come from ideas in pure maths much after its initial development. This includes RSA cryptography coming from number theory, or quantum mechanics coming from Lie theory. Thus, it may become useful in the future, even if it is not clear how in the present. Even so, there are still many topics in pure maths that do not have strict applications. However, different ideas and mathematical tools can arise from it, which may be useful. But most importantly, it is the curiosity, beauty and appeal of topics in pure maths that drive pure mathematicians. Pure maths is extremely technical and often leads to ideas being extremely abstract and difficult to understand even for mathematicians, let alone the general public. However, I hope that fractals give a visual overview of what mathematicians find captivating about maths. Fractals are visually beautiful to look at, and we are curious to know how to construct them, various properties of them, and what we can learn about it. Most topics in pure maths cannot be visualised like this, but nonetheless, the idea remains the same. We love learning about the details of some topic in maths and finding beauty within it.
Akito Koike
The University of Sydney