Abstract: Can you solve this puzzle? If you can, great work! You’ll have proven an important mathematical result and gained an intuitive understanding of what a semigroup presentation is. Finding a presentation is a perfect example of one of mathematics greatest strengths: reducing the complexity of a system to the fundamental pieces needed to describe it.
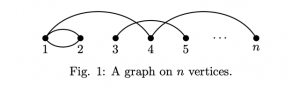
Picture a graph consisting of n vertices in a row labelled 1 through n and some number of edges connecting these vertices, such as in Fig. 1.
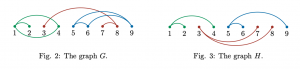
An edge between two vertices a and b where a < b will be written as (a b). There may be more than one edge between a pair of vertices. We will refer to the connected components of this graph as blocks (i.e., the collections of vertices that are connected by a series of one or more edges). Notice how it’s possible for two graphs with different sets of edges to have the same blocks, as in Fig. 2 and Fig 3. An edge sequence is a list of edges in some order. A graph can have multiple edge sequences that represent its edge set.
Say we have two graphs G and H with nine vertices, where:
– The graph G (Fig. 2) has an edge sequence (1 2), (3 8), (7 8), (1 4), (5 9), (1 4), (6 9), (5 6)
– The graph H (Fig. 3) has an edge sequence (1 2), (1 4), (3 7), (3 8), (5 6), (5 9)
Both G and H have blocks {1, 2, 4}, {3, 7, 8} and {5, 6, 9}. So, what’s the puzzle?
Here are the rules:
- The order of any two consecutive edges in a sequence can be swapped.
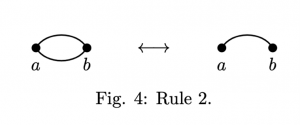
- Any consecutive pair of edges which are identical can be replaced by a single such edge (Fig. 4).
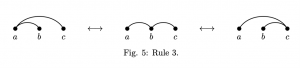
- Any consecutive pair of edges that span the same three vertices can be replaced by any other pair that also spans those vertices (Fig. 5). For example, the pair (1 2), (2 3) can be replaced by either (1 2), (1 3) or (1 3), (2 3).
Using these rules, can you transform G’s edge sequence into H’s? Let’s call two edge sequences equivalent if they correspond to graphs with the same blocks. Can you think of a method that will work to turn any two equivalent edge sequences into the same sequence? I’ve provided a solution below, but before you read it, try and come up with one yourself. Chances are it will be better than mine!
This puzzle is analogous to proving a presentation for the semigroup of equivalence relations on a set [1, Theorem 2]. Think of this as the collection of all possible partitions of a set, where two partitions can be combined by merging any overlapping blocks to form a new partition. But what’s a presentation? A presentation reduces a semigroup to a set of ingredients and a set of rules that can describe all combinations of those ingredients. In our puzzle, the ingredients are the edges. They represent a block of two vertices, and some combination of edges can be used to create any configuration of blocks in a graph. The goal of the puzzle is to prove the above three rules are sufficient to change any edge sequence into any other equivalent sequence.
A useful technique for proving a presentation is defining the normal form of each object in the set. The normal form acts like an archetype of all the sequences of ingredients that correspond to the same object. This provides a clear objective for the proof: show that all sequences can be turned into their equivalent normal form. In our puzzle, H’s edge sequence is an example of the normal form I have defined for graphs that have the blocks {1, 2, 4}, {3, 7, 8} and {5, 6, 9}. To find the normal form of a given set of blocks, choose k-1 edges to represent each block, where k is the size of that block. These will be all possible pairs of vertices in that block that include the least vertex in that block. Then, the representatives for each block are placed in ascending order.
Solution:
For the general solution, the steps describe the process of turning any sequence into its corresponding normal form. The numbered items show the specific solution for turning G’s sequence into H’s (while providing an example of the general solution).
Step 1: Use Rule 1 to sort G’s edge sequence into ascending order.
- (1 2), (1 4), (1 4), (3 8), (5 6), (5 9), (6 9), (7 8).
Step 2: Starting with the first edge in the sequence (a b), check if there exists in the sequence some edge with the form (b c) if b < c or (c b) if c < b for some c which is not equal to a (for simplicity, we’ll assume b < c). If there is, record the place of (a b) in the sequence, use Rule 1 to shift (a b) forward in the sequence until it hits (b c), use Rule 3 to replace the pair (a b), (b c) with (a b), (a c), then shift them both back into the recorded place for (a b). Repeat this step until there are no more edges with the form (b c) for some c not equal to a (In our example, the first edge that satisfies this is (3 8), so we start there).
- (1 2), (1 4), (1 4), ____, (5 6), (5 9), (6 9), (3 8), (7 8).
- (1 2), (1 4), (1 4), (5 6), (5 9), (6 9), (3 8), (3 7).
- (1 2), (1 4), (1 4), (3 8), (3 7), (5 6), (5 9), (6 9), ____, ____.
Step 3: Repeat Step 2 for the next edge in the sequence until all edges have been checked (In our example, the next edge to satisfy Step 2 is (5 6)).
- (1 2), (1 4), (1 4), (3 8), (3 7), ____, (5 9), (5 6), (6 9).
- (1 2), (1 4), (1 4), (3 8), (3 7), (5 9), (5 6), (5 9).
- (1 2), (1 4), (1 4), (3 8), (3 7), (5 6), (5 9), (5 9), ____, ____.
Step 5: Use Rule 1 again to sort into ascending order and use Rule 2 to remove duplicates. We now have our normal form.
- (1 2), (1 4), (3 7), (3 8), (5 6), (5 9).
Why will this always work? Performing Step 2 on each edge in ascending order ensures all edges will contain the least vertex in their block after Step 3. Then, sorting and removing the duplicates gives us our normal form.
References:
[1] FitzGerald, Desmond G. (2003). ‘A presentation for the monoid of uniform block permutations’. Bull. Austral. Math. Soc. 68.2, pp. 317–324.
Luka Carroll
Western Sydney University