When I tell people that I’ve been doing a research project on knots, some people say ‘oh that’s cool’ or ‘that sounds interesting’, but most people are just not sure how to react.
Usually when we think of maths, numbers are the first thing which comes to mind, some equations, a bit of geometry here and there, but knots? Well, there is actually a branch of mathematics called knot theory; let’s take a brief look at what it is.
First, what is a mathematical knot? Are your shoelaces a knot? Is a rubber band a knot? To start with, mathematical knots cannot have loose ends, so your shoelaces, which don’t have both ends attached, are not mathematically considered knots! A rubber band, on the other hand, is a knot. In fact, it’s the simplest type of knot, an unknot, a knot with no crossings. Imagine a pipe-cleaner, you twist it up however you like and then glue its two ends together (so they are permanently attached), then what you have is a knot.
One of the fundamental questions of knot theory; how can we tell if two knots are the same? Or different? This might seem obvious, but imagine if you and I each have a piece of string which we twist up as much as we like and then glue the ends together so we each create a knot. Now maybe it’s a bit harder to tell if they’re the same or not?
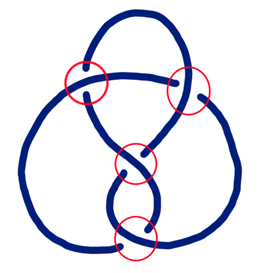
One way we can identify knots is by the number of crossings. For example, the knot shown below (called the figure eight knot) has four crossings, circled in red.
Considering a rubber band again, if I twist it up a lot, then doesn’t it have many crossings? But in fact, we can always undo these, to get back to the same simple circle. So in order to identify the number of crossings, we need to untwist a knot as much as we can so it has as few crossings as possible. But how can we tell when we have reached the minimum number of crossings? Well, this turns out to be an open problem, there’s no known algorithm which takes any general knot diagram and tells you the minimum number!
Things like the minimum number of crossing of a particular knot are known as knot invariants, properties which are always the same for a particular knot. There are other knot invariants, for example, we can do calculations on a knot to get a polynomial which we can use to identify knots (called knot polynomials).
So, where do we use all this? Actually, knot theory comes up in many areas, in maths of course, but also in fields like statistical mechanics, as well as in understanding DNA. We’ve just scratched the very surface of knot theory here, but hopefully I’ve got you a bit interested, and maybe the next time you look at a rubber band you’ll view it a little differently.
Emma McQuire
Monash University