Various generalisations exist of the Kepler Problem beyond flat everyday geometry to more exotic geometries. An example of such a generalisation is the Kepler-Heisenberg Problem. By understanding the symmetries of the energy function (Hamiltonian), we are able to reduce the complexity of solving the equations of motion. We can compute special invariant quantities, known as rotation numbers, and classify the orbits.
Throughout human history, we have been fascinated by the motion of the stars in the night sky. Watching them wander in periodic and regular patterns, and wondering whether we could predict their future motion. In essence, this has historically been one of the motivational pillars behind the development of mathematics and classical mechanics.
In the 1610s, Johannes Kepler formulated the well celebrated Three Laws of Planetary Motion, by studying astronomical data of the motion of the planets and sun in our solar system recorded by Tycho Brahe. His work set the sun as a fixed point and described the orbits of the planets as tracing out ellipses. The results of Kepler can be codified into a mathematical formula known as a Hamiltonian, which physically encodes the energy of a body orbiting around the central sun. From this we are able to find the equations of motion for the coordinates and momenta, and solve for the trajectories of motion. This is known as the Kepler Problem.
From the outside, we often view mathematics as a dry and rigid subject, involving number crunching and following formulaic algorithms. However, from a Mathematician’s perspective, it is often the complete opposite, rather a subject that requires imagination of abstract quantities. What sort of physics would a Keplerian system have beyond the everyday geometry of three-dimensional Euclidean space? One geometry of interest is the Heisenberg geometry. Solving the equations of motion for the Kepler problem posed on this geometry is known as the Kepler-Heisenberg problem. Formulation of the problem and prior analysis has been undertaken by Montgomery, Shanbrom, and Dods.
A special property of the Kepler problem is that every negative energy orbit is periodic. That is, after a finite amount of time orbiting the central sun, the body returns to its initial state. For general Hamiltonian systems, including the Kepler-Heisenberg problem, it is not true in general that all bounded orbits are periodic.
Symmetries and conserved quantities allow us to greatly simplify the analysis of dynamical systems. In fact, if a system has sufficiently enough independent conserved quantities, then we are able to describe our system in terms of invariant quantities known as `rotation numbers’. For those interested, this follows from an important theorem in Hamiltonian mechanics known as the Liouville-Arnold Theorem.
Imagine a mass on a spring that lies on a horizontal two-dimensional tabletop, with the spring fixed to the centre of the table. The mass is able to `bob’ on the spring as well as rotate around the centre point. In this context the rotation number corresponds to the amount of rotation per bob. If the rotation number is rational, then the system is able to return to its initial condition in a finite amount of time, and the orbit is periodic. However, If it is irrational, then the system will not return to its initial condition in finite time. The orbit is quasi-periodic.
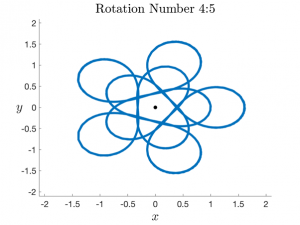
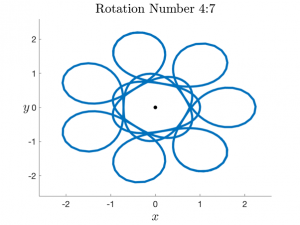
For the zero energy subsystem of the Kepler-Heisenberg problem, we find there are three conserved quantities: energy, angular momentum, and a quantity known as the dilational momentum. The dilational momentum can be interpreted as momentum causing the body to spiral in/away from the central sun. In this project we were able to find and compute two important invariant quantities, the rotation number and dilation number.
When the dilational momentum is zero, the dilation number is zero and there exists periodic orbits with rational rotation numbers. The corresponding orbits form bizarre and mesmerising patterns, resembling criss-crossing knots and flower petals.
In general, it turns out that the rotation and dilation numbers do indeed correspond to physical dilation and rotation of fundamental segments of the orbits, after each `bob’ along the vertical z-axis. This behaviour gives rise to the self-similar orbits of the zero energy Kepler-Heisenberg problem.
References:
[1] R. Montgomery and C. Shanbrom, “Keplerian Dynamics on the Heisenberg Group and Elsewhere,” in Geometry, Mechanics, and Dynamics, Fields Institute Communications, pp. 319–342, New York, NY: Springer New York, 2012.
[2] F. Diacu, “Relative Equilibria in the 3-dimensional Curved n-body Problem.” Memoirs of the American Mathematical Society, Volume 228, Number 1071, Providence, Rhode Island: American Mathematical Society, 2013.
[3] V. Dods and C. Shanbrom, “Self-Similarity in the Kepler–Heisenberg Problem,”Journal of nonlinear science, vol. 31, no. 3, 2021
Example periodic orbits:
Jonathan Skelton
The University of Sydney